Volatilität: Clustering und (G)ARCH-Modelle

In der Finanzökonomie ist Volatilität ein wesentliches Merkmal vieler Graphen sowohl von Aktien, Rohstoffen als auch Kryptowährungen. Diese Graphen werden wir im Folgenden als 'Finanzzeitreihen' bezeichnen.

Nach Entstehung der Efficient Market Hypothesis stellten Akteure der Finanzmarktforschung die Behauptung auf, Theorien wie die Random-Walk-Theorie sowie die darin befindliche brownsche Bewegung bilden Finanzmärkte nicht in ihrer Vollständigkeit ab: Unerwartete Ereignisse fallen aus der Norm und können über die Standardabweichungen der Theorien, die von zufälligen Bewegungen am Markt ausgehen, nicht korrekt abgebildet werden.

Solche Ereignisse nennen wir Black Swan Events. Schonmal einen schwarzen Schwan gesehen? Vermutlich nicht. Daher der Name: Black Swan Events beschreiben Phänomene, die so selten oder gar einzigartig sind, dass deren Einfluss auf den Markt nicht anhand von historischen Präzedenzfällen eingeschätzt werden kann. Prominente Beispiele sind der weltweite Lockdown zu Corona-Hochzeiten im April 2020, die Finanzkrise im Jahr 2008 oder der Bombenabwurf über Hiroshima und Nagasaki.

Ein schwarzer Schwan - Eine Metapher für ein Ereignis, das so selten oder einzigartig ist, dass es nicht vorhergesagt werden kann.

Modelle, die sich auf Volatilität spezialisieren, gedenken, solche Ereignisse zwar nicht vorauszusagen, deren zukünftigen Einfluss aber besser modellieren zu können. Zwei dieser Modelle sind das ARCH- sowie das GARCH-Modell, die speziell zur Modellierung der Varianz von Zeitreihen entwickelt wurden.

Volatility Clustering bezeichnet die Beobachtung, dass große Schwankungen der Aktienkurse dazu neigen, auf große Schwankungen zu folgen, während kleine Schwankungen mit kleinen Schwankungen einhergehen. Dies widerspricht der Annahme einer konstanten Volatilität und zeigt, dass Volatilität selbst persistent sein kann.

Das Autoregressive Conditional Heteroskedasticity (ARCH)-Modell wurde 1982 von Robert Engle entwickelt, um Volatility Clustering explizit zu modellieren. Es beschreibt, dass die aktuelle Volatilität einer Finanzzeitreihe von vergangenen Marktschwankungen abhängt.

ARCH-Modelle nutzen vergangene Abweichungen (Fehlerterme), um die zukünftige Schwankungsintensität (Varianz) zu prognostizieren.

Die Grundidee ist: Wenn in der Vergangenheit große Schwankungen auftraten, steigt die Wahrscheinlichkeit für zukünftige große Schwankungen. Wenn die Märkte sich in der Vergangenheit ruhig verhielten, bleibt die Volatilität tendenziell niedrig.

Mathematisch formuliert sieht das ARCH(q)-Modell so aus:

$\sigma_t^2 = \alpha_0 + \sum_{i=1}^q \alpha_i \epsilon_{t-i}^2$

• • Risikomanagement: Berechnung von zukünftigen Marktschwankungen zur besseren Einschätzung von Risiken.
• • Portfoliomanagement: Anpassung der Anlagestrategie an volatilere Marktphasen.
• • Optionsbewertung: Schätzung zukünftiger Schwankungen für faire Optionspreise.

Die Generalized Autoregressive Conditional Heteroskedasticity (GARCH)-Modelle sind eine Erweiterung des ARCH-Modells. Sie berücksichtigen nicht nur vergangene Fehlerquadrate, sondern auch frühere Volatilitätswerte, um die zukünftige Schwankungsbreite noch besser zu schätzen.

Während ein ARCH-Modell nur große Fehler aus der Vergangenheit berücksichtigt, fügt das GARCH-Modell einen weiteren Faktor hinzu: Es schaut auch darauf, ob die Volatilität in der Vergangenheit hoch oder niedrig war. Das bedeutet:

Wenn die Volatilität in der Vergangenheit hoch war, könnte sie weiterhin hoch bleiben. Wenn sich die Märkte zuletzt beruhigt haben, könnte sich dieser Trend fortsetzen.

Die Formel eines GARCH(p,q)-Modells sieht so aus:

$\sigma_t^2 = \alpha_0 + \sum_{i=1}^q \alpha_i \epsilon_{t-i}^2 + \sum_{j=1}^p \beta_j \sigma_{t-j}^2$

• • Genauere Vorhersagen: Da es nicht nur vergangene Fehler, sondern auch vergangene Volatilität betrachtet, kann es Trends besser erkennen.
• • Glattere Modellierung: ARCH-Modelle benötigen oft viele Parameter, um Marktschwankungen gut abzubilden. GARCH-Modelle reduzieren diese Komplexität und liefern trotzdem bessere Ergebnisse.

• • Handelsstrategien: Identifizierung volatiler Marktphasen für kurzfristige Trades.
• • Stress-Tests: Modellierung, wie Märkte in extremen Situationen reagieren könnten.
• • Risikosteuerung: Bessere Anpassung von Stop-Loss-Strategien basierend auf Marktvolatilität.

Um nun das ARCH- oder GARCH-Modell selbst zu nutzen, um unsere potenziellen Investments bezüglich Volatiliy-Clustering zu modellieren, braucht es nun schon etwas mehr technisches Know-How:

Zunächst benötigen wir jede Menge historische Preisdaten des Basiswerts, den wir zu analysieren versuchen. Hier empfehle ich mindestens 250, idealerweise 500 Tage an Preisdaten, um eine robuste Analyse basierend auf vergangenen Price Movements durchführen zu können.

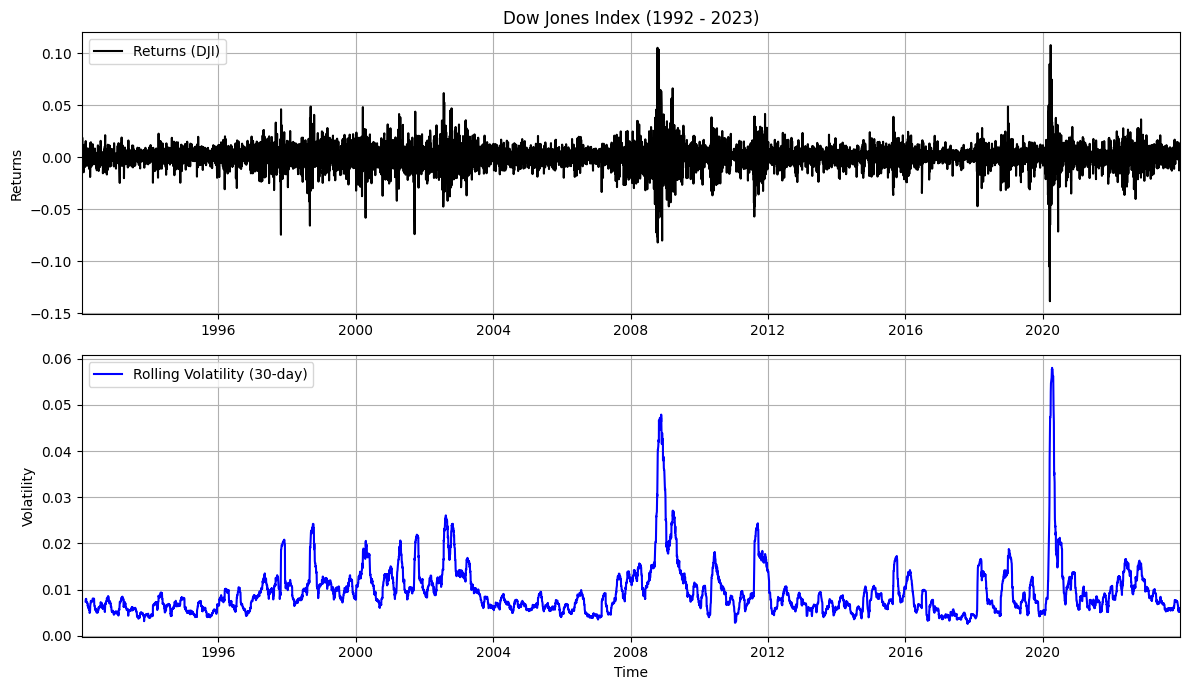
Der tatsächliche Kursverlauf des Dow Jones im Vergleich zur gleitenden Volatilität des Kursverlaufs.

Die tatsächlichen Berechnungen für unser Modell führen wir idealerweise programmatisch – beispielsweise mit Python – durch, da wir bspw. die Renditen für einzelne Tage basierend auf dem aktuellen und vorherigen Tag berechnen und Renditen außerdem auf Stationarität prüfen müssen, sollten wir das GARCH-Modell verwenden wollen.

Da eine genaue Schritt-Für-Schritt Anleitung für die Verwendung dieses Modells den Rahmen dieses Artikels vollständig sprengen würde, kann ich stattdessen bloß das folgende Video empfehlen. Insbesondere für technisch etwas versiertere Leser ist der Ablauf einer solchen Modellierung in einem Video ohnehin deutlich einfacher nachzuvollziehen.

Solltet ihr euch dennoch für eine detaillierte Erklärung zur Verwendung dieser Modelle durch mich interessieren, meldet euch gern über meine Socials bei mir. Bei genügend Meldungen kann ich mir gut vorstellen, noch einmal einen gesonderten Artikel zu schreiben, ggf. sogar mit Einbettung des Modells in ein Spreadsheet, das ihr kopieren und verwenden könnt.

Finanzmärkte sind komplex und können, auch, wenn es verlockend klingt, nicht stump über die Behauptung zufälliger Kursschwankungen gelöst werden. Auch Modelle, die sich nun auf Volatilität im Markt konzentrieren, sind nicht der heilige Gral der Chartanalyse. Dennoch zeigen sie auf, dass Konzepte wie die Random-Walk-Theorie um zusätzliche Parameter erweitert werden mussten, um eine holistischere Marktprognose vornehmen zu können.

Wie wir in den nächsten Kapiteln lernen werden, war auch dies noch nicht das Ende der Fahnenstange.