Fibonacci-Retracements und ihre Implikationen

Fibonacci Retracements sind heutzutage eines der wichtigsten Mittel der Kurszielbestimmung für die meisten Charttechniker und gehören ins Kern-Repertoir eines jeden von ihnen. Doch was sind Fibonacci Retracements, wo kommen sie her und was bedeuten sie für die Finanzwelt überhaupt?

Fibonacci Retracements beruhen auf der berühmten "Fibonacci-Folge", auch Fibonacci-Zahlen genannt. Die Fibonacci-Zahlen gehen auf den italienischen Mathematiker Leonardo Fibonacci zurück, der im 13. Jahrhundert, genauer gesagt um das Jahr 1202, in seinem "Buch der Rechenkunst" zum ersten Mal von ihnen sprach. Fibonacci lebte zu einer Zeit, zu der die Mathematik als hohe Kunst und Hobby vieler junger Menschen nicht nur erstaunlich angesehen war sondern auch öffentlich zelebriert wurde.

Fibonacci versuchte stets, Sachverhalte, die er beobachtete, mathematisch zu erklären und war seiner Zeit darin voraus, diese Sachverhalte aus der echten Welt über Vereinfachungen berechenbarer zu machen. Zu einem dieser Sachverhalte, den er als Grundlage für die später nach ihm benannte Zahlenfolge nutzte, stellte er sich folgende Frage:

Wie viele Kaninchen entstehen innerhalb eines Jahres aus einem einzigen Paar?

Diese Frage bietet, auch wenn sie erst einmal simpel klingt, jede Menge Schlupflöcher für unerwartete Komplexität. Nicht jedes weibliche Kaninchen ist zum selben Alter geschlechtsreif - Austragungszeiten variieren, ein jedes Paar könnte 2 Weibchen oder 2 Männchen zur Welt bringen, manche Tiere möchten sich eventuell nicht verpaaren, andere sterben zu "unvorhersehbaren" Zeitpunkten.

Daher griff Fibonacci auf einige Vereinfachungen zurück, um seiner eigenen Fragestellung und deren Lösung Herr zu werden:

• • Jedes Paar wirft nur exakt 1x pro Monat 1 neues Paar von Männchen und Weibchen
• • Ein jedes Paar bekommt ab dem zweiten Lebensmonat Nachwuchs
• • Die Tiere befinden sich in einem abgeschlossenen Raum, sodass keines die Population verlässt oder von außerhalb des Raums hinzukommt
• • Alle Kaninchen sind unsterblich
• • Das erste Paar beginnt den ersten Monat trächtig

Lasst uns also Schritt für Schritt die Ergebnisse seines Gedankenexperiments durchgehen:

• • 1. Monat: Es existiert 1 trächtiges Paar
• • 2. Monat: Es existieren 2 Paare, eines noch zu jung
• • 3. Monat: 3 Paare (erstes Paar erneut trächtig, zweites jetzt auch trächtig)
• • 4. Monat: 5 Paare (3 vom Vormonat trächtig, 1 zu jung)
• • 5. Monat: 8 Paare

Dies lässt sich unendlich lang fortführen, doch nach einigen Iterationen fiel Fibonacci auf, dass die Anzahl der Paare eines Monats der Summe seiner beiden Vormonats-Paare entspricht. Im 5. Monat addieren wir die Zahl des 4. (5) + die Zahl des 3. Monats (3) und erhalten 8. Darauf folgen 13. Darauf 21, 34, 55, 89, 144 und schließlich 233 Kaninchen im ganzen Jahr.

Mit fortlaufender Zeit bemerkte man immer häufiger, dass die Fibonacci-Folge in der Natur allgegenwärtig ist: Die Anzahl der Blütenblätter der Agave sind eine Fibonacci-Zahl. Die Kerne einer Sonnenblume wachsen in beide Richtungen in je 34 und 55 Spiralen: Beides Fibonacci-Zahlen. Tannenzapfen folgen dem selben Muster und sogar Nautilus-Muscheln wachsen nach dem Fibonacci-Muster nach außen, um die einzelnen Kammern ideal zum Ab- und Auftauchen füllbar zu gestalten.

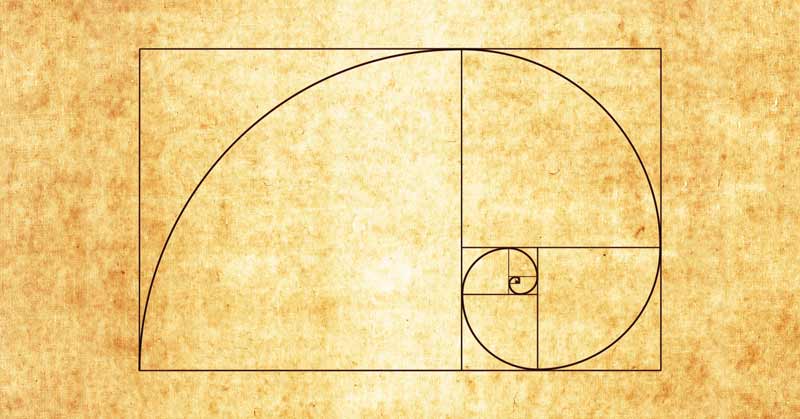
Ein Kachelmuster, in seiner Breite basierend auf der Größe der zugehörigen Fibonacci-Zahl. Quelle: simplifaster.com

Teilt man eine Fibonacci-Zahl durch ihren Vorgänger, erhält man immer den Wert 1.618 - das Größenverhältnis zwischen verschiedenen Gesichtsmerkmale des Menschen.

Eine der wichtigsten Eigenschaften der Fibonacci-Folge ist nun das eben genannte Verhältnis zwischen aufeinanderfolgenden Zahlen. Wenn man eine Zahl der Reihe durch ihre Vorgängerzahl teilt, nähert sich das Ergebnis asymptotisch dem sogenannten Goldenen Schnitt, der etwa 1,618 beträgt. Dieses Verhältnis ist als Phi (ϕ) bekannt und wird oft als „perfekte Proportion“ bezeichnet.

• • 23,6% (berechnet durch Division einer Fibonacci-Zahl durch die Zahl zwei Stellen weiter)
• • 38,2% (berechnet durch Division einer Zahl durch die Zahl eine Stelle weiter)
• • 61,8% (Division einer Zahl durch die nachfolgende Zahl)
• • 78,6% (Quadratwurzel aus 61,8%)

Du fragst dich nun vielleicht, weshalb du seit 5 Minuten einen Artikel über Naturwissenschaften liest, wo du doch eigentlich mehr über Finanzmärkte lernen wolltest. Aufgrund der Tatsache, dass die Fibonacci-Folge auf sämtliche Teile der Natur anwendbar und darin auffindbar sind, liegt die Vermutung nahe, dass sie sich ebenso nützlich auf die Muster der menschlichen Psychologie und ihrer Entscheidungsfindung anwenden lässt.

Insbesondere im Zusammenspiel mit dem Elliot-Wellen-Prinzip, welches wir uns im nächsten Kapitel gemeinsam anschauen, bildeten sich gezielt auf dieser Basis Handelsstrategien vieler Trader und Investoren.

Ein Fibonacci-Retracement ist ein technisches Analysewerkzeug, das auf den oben genannten Verhältnissen basiert. Es wird verwendet, um potenzielle Wendepunkte im Preisverlauf eines Wertpapiers bzw. Basiswerts zu identifizieren.

Trader nutzen Fibonacci-Retracements, um potenzielle Unterstützungs- und Widerstandsniveaus zu bestimmen. Diese Niveaus sind Stellen, an denen sich der Kurs mit hoher Wahrscheinlichkeit umkehren oder zumindest verlangsamen kann.

• 1. Identifizierung: Ein markanter Trend ist identifiziert.
• 2. Markierung: Hoch- und Tiefpunkte werden im Kurs markiert.
• 3. Anwendung: Retracement-Tool wird auf den Chart gelegt.
• 4. Automatische Anzeige: Linien bei 23,6%, 38,2%, 50%, 61,8%, 78,6% werden angezeigt.
• 5. Beobachtung: Kursverhaltens an diesen Levels muss beobachtet werden.
• 6. Einstiegssignale: Umkehrverhalten signalisiert Validierung

Angenommen, eine Aktie steigt von 100 € auf 200 € und beginnt dann zu korrigieren. Die Fibonacci-Retracements würden die folgenden potenziellen Unterstützungsniveaus anzeigen:

• • 23,6% Retracement: 176,4€
• • 38,2% Retracement: 161,8€
• • 50,0% Retracement: 150,0€
• • 61,8% Retracement: 138,2€

Falls der Kurs auf 161,8 € fällt und dort eine Stabilisierung zeigt, könnte dies ein potenzieller Punkt sein, an dem die Korrektur endet und der Kurs wieder steigt.

Fibonacci-Retracements sind ein wertvolles Werkzeug für Trader und Investoren, um potenzielle Umkehrpunkte im Markt zu identifizieren, liefern aber keine hundertprozentig zuverlässigen Prognosen. Andere Faktoren können die Kursbewegungen stark beeinflussen, weshalb Fibonacci-Retracements - ähnlich wie andere Theorien und Prinzipien, die wir uns in den letzten Kapiteln angesehen haben - nicht isoliert und allein angewandt werden, um zu versuchen, Kurse zu prognostizieren.

Nachdem wir uns ein fundiertes Hintergrundwissen zur Finanzmarkttheorie aufgebaut haben, betrachten wir nun im nächsten Kapitel ein Analyse- und Prognosemodell an, das eng mit Fibonacci-Retracements arbeitet und uns Einblicke dahingehend verschafft, wie auch wir diese Retracements für unsere Handelsentscheidungen nutzen können.